PRECIOS DEL ORO EN TIEMPO REAL
INVERTIR EN ORO

CFDs sobre oro: operar con más oro por menos dinero
Los CFDs sobre oro son un derivado financiero que nos permite apalancarnos a la hora abrir posiciones. Gracias al factor ...

¿Invertir en oro es inteligente? 7 claves
¿Invertir en oro es inteligente? El valor del oro y su extensa historia, que abarca miles de años y está ...

Invertir en oro para la jubilación
Invertir en oro para la jubilación suele despertar grandes dudas y temores. No hay problema, repasemos juntos las ventajas e ...

Invertir en oro físico: 8 claves para proteger tu patrimonio
Invertir en oro físico es una opción muy valorada por muchos inversores a lo largo de todo el mundo. El ...

Invertir en oro: Cómo proteger tus ahorros de la inflación
Invertir en oro se puede llevar acabo de muchas maneras diferentes, y si eres novato en el campo de la ...
PREGUNTAS

¿Cuántos gramos son una onza de oro?
En términos técnicos, una onza es la décima parte de una libra avoirdupois (28.349 gramos), y también es una moneda ...

Oro en marte: ¿Es posible? ¿Hay evidencias científicas?
Desde hace mucho tiempo, se ha especulado sobre la existencia de oro en Marte. Aunque la mayoría de la gente ...

Oro falso ¿Cómo detectarlo? Guía fácil
El oro falso es un problema que afecta a muchas personas en todo el mundo. Se trata de una sustancia ...

Oro rosa ¿Qué es y cómo distinguirlo?
El oro rosa es una aleación de oro y cobre que se caracteriza por su color rosado. Aunque el oro ...

¿Dónde comprar monedas de oro?
¿Dónde comprar monedas de oro? En este artículo te explico cómo. Desde el inicio de la pandemia del coronavirus, el ...
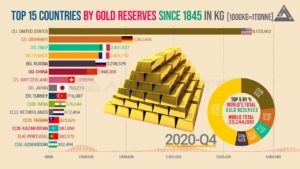
¿Cuánto oro hay en el mundo?
El oro es uno de los elementos más valiosos del mundo, y su precio refleja eso. Según el World Gold ...

¿Cómo saber si hay oro en un río?
La perspectiva de encontrar oro en un río es emocionante, pero ¿Cómo se sabe si hay oro en un río ...
Óxido de oro: ¿Cómo se forma? ¿Qué usos tiene?
Óxido de oro: ¿Cómo se forma? ¿Qué usos tiene? El óxido de oro es un compuesto químico de oro y ...